Fortunately, I spotted my mistake before suffering the indignity of having somebody point it out and I updated the original post with a warning that the so-called "analysis" was nonsense. I also promised to correct it - so here we go...
The circuit under consideration is shown in the image below...
 We start the analysis by noting that the voltage at the non-inverting input to the op-amp can be related to the input voltage using the potential divider equation (it was at this stage I made one of the dumb mistakes in my previous botched analysis)...
We start the analysis by noting that the voltage at the non-inverting input to the op-amp can be related to the input voltage using the potential divider equation (it was at this stage I made one of the dumb mistakes in my previous botched analysis)...
Ideal operation of the op-amp (which here is set up as a voltage follower) will force the voltage difference between the inputs to zero, such that...

(Microsoft's Equation Editor has done a pretty poor job of laying out this equation - but life is rather too short to do anything about it!!)
Next we turn our attention to i2...

Now we have both currents, we're able to solve for the input impedance of the circuit ...

which is solved by substituting our solutions for the two currents...

This impedance is that of a series combination of resistor and inductor, with another resistor "shunting" the inductor, as shown in this equivalent circuit...

The Gyrator is seen to emulate a "virtual inductor" having value L = (R2-R1)R1C, in series with a resistor Rs = R1, shunted by a resistor Rshunt=R2-R1. This virtual inductor can easily have large value - a value so high as to be impractical to achieve using a physical inductor.
Simplistic descriptions of the Gyrator have an approximate solution for the "virtual inductor" (which is the same as that presented in my erroneous "analysis") but miss the shunt resistance. In practical cases, R2 >> R1, such that the simple solution is a very good approximation of the correct analysis presented here. But that's no excuse - an analysis (even one published in such informal surroundings as this blog) must be right.
QED Hi Hi
...-.- de m0xpd

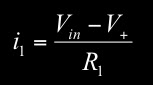



No comments:
Post a Comment